いとこが公務員試験を受けるので、先日実家に帰った時に勉強を教えてたんですけど、僕が教えられるのは「数的処理」と「数学」なので(もともと文系なのですが)、「論理」とか「仕事算」とか「確率」とか「速さ」とか「因数分解」とかいろいろ教えていて、いとこが一番参考になったと言ったのが「N進法」だったんですね。
目次
参考書のN進法の解き方が割り算をして余りを出していくのはなぜか分かりづらいという方へ・二進法の解き方
既存の参考書の解き方だと、なんか割り算して余りを出してみたいに書いてありますが、なぜそうなるのかが分かりづらい方もいると思います。
今回直観的に分かるように説明していきたいと思います。
N進法で一番代表的なのが「二進法」で、これはコンピュータが使っている考え方なんすね。
N進法を解くときはオンオフができるスイッチがついている「電球」をイメージするといいと思います。

コンピュータは僕らみたいに、千円とか一万円みたいな、10の倍数で増えていく「十進法」を使っていないんです。
なぜなら、二進法を使えば、オンオフのスイッチだけで、全ての数字を表すことができるからです。
まず、十進法のスイッチは
…10000、1000、100、10、1
となっています。
対して、ニ進法のスイッチは
…128、64、32、16、8、4、2、1
なんですね。
10進法が10をかけていき(10×10=100)(10×10×10=1000)スイッチを増やしていくのに対し、2進法は2をかけてスイッチを増やしていきます(2×2=4)(2×2×2=8)
例えば、100。という数字。これを二進法で表してみましょう。
まず64のスイッチが1つ入ります。100-64=36ですね。
次に32のスイッチが1つ入ります。36-32=4ですね
次に4のスイッチが一つ入ります。4-4=0ですね。0になったら終わりです。
これによりスイッチが入ったところは1、入らなかったところは0にすると、
1 1 0 0 1 0 0
64 32 16 8 4 2 1
となります。
よって、100を二進法で表すと「1100100」となります。
逆もできますね。
二進法を十進法に直してみましょう。二進法の「1111000」を10進法にすると
1 1 1 1 0 0 0
64 32 16 8 4 2 1
だからテストの時に、用紙にスイッチを先に書いてしまえばいいんです。そうすれば、割り算とかしなくても答えを出せます。
→林修先生の名言ランキングまとめ【おすすめ・仕事・努力・人間関係・恋愛・本】はコチラ
五進法の解き方・二進法との違い【n進法の変換のやりかた】
では五進法などの場合はどうなるか。まず五進法のスイッチは下のようになります
…625、125、25、5、1
どんどん5を掛けていってるんですね。(お気づきかと思いますが、一番右のスイッチは毎回1になります。これは、「5に0の塁乗をしているから」なのですが、まあ理屈抜きにそう言うものだと覚えても大丈夫です)
二進法との違いは、五進法の場合は、スイッチを4回まで押せます。例えば、右から2つめの5のスイッチを4回押すと、(5×4)で20ポイント入ります。
(N-1)回スイッチを押せるわけです。十進法は9回スイッチを押せます。
よって五進法の(40)は十進法では(20)となります。
4 0
5 1
では、十進法の104を五進法で表すとどうなるでしょうか?
…625、125、25、5、1
まず、25のスイッチを4回押せます。104-100で4残ります。
4しかないので、5のスイッチは押せません。
次に、1のスイッチを4回押せます。
よって、
4 0 4
25 5 1
となり、404が正解となります。
今まで書いて来た流れを計算式にすると、「割って余りをだして」みたいな参考書の解き方になるわけです。
ただそれが直観的に分かりづらい人は、僕のようにスイッチをまず書いてしまって、オンオフしていけば、答えはすぐに出せます。
→林修氏の名言「1カ月頑張れるかどうかで人生が変わる」【受験・勉強】はコチラ
N進法は一度十進法に直してしまえば、掛け算でも簡単に解けます(公務員試験も入試問題もサービス問題)
N進法は、今回のように一度スイッチを書いて十進法に直してから計算すれば、掛け算でも割り算でも簡単に解けます。
N進法がテストで出たら、チャンス問題だと思ってもらって大丈夫です。
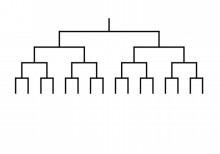
→16人のトーナメントで優勝者を決めるのに何試合必要か?はコチラ
→『家庭教師理論』~短期間でTOEICの点数を200点上げる方法~はコチラ
→『連鎖理論』~公募コンテストで最優秀賞を獲る方法~はコチラ













数学を学びなおしたいと思っている40代ですが、2進法が学んだ記憶すら無いほど(笑)チンプンカンプンで、、。どんな解説を見てもピンとこない文系人間ですが、初めて光が見えました。わかりやすい解説ありがとうございます!!
mickyさん、コメントありがとうございます!お役に立ててうれしいです!
数学は大人になってから学びなおすと、新鮮で面白いですよね!
2進法は一度パターンを理解すると、スラスラ解けるようになると思います(*’▽’)